StackingCVRegressor: stacking with cross-validation for regression
An ensemble-learning meta-regressor for stacking regression
from mlxtend.regressor import StackingCVRegressor
Overview
Stacking is an ensemble learning technique to combine multiple regression models via a meta-regressor. The StackingCVRegressor extends the standard stacking algorithm (implemented as StackingRegressor) using out-of-fold predictions to prepare the input data for the level-2 regressor.
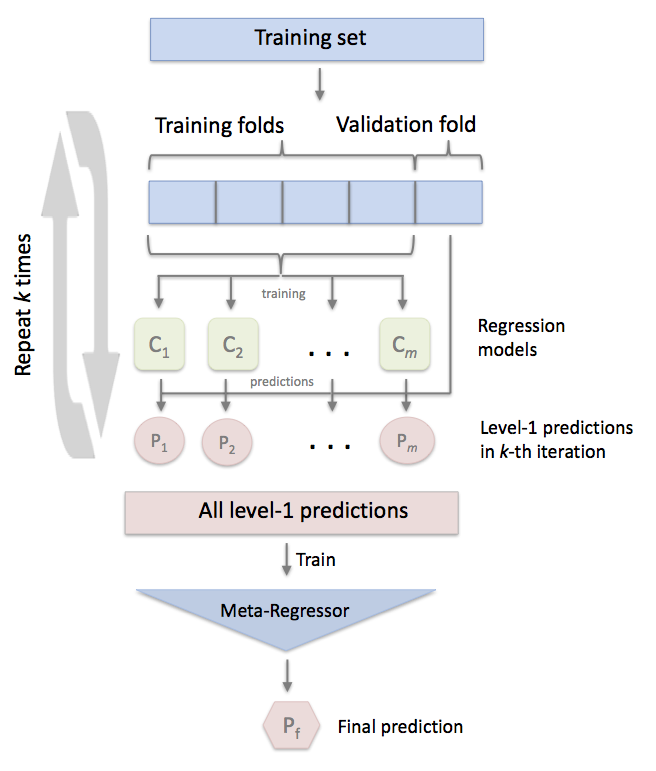
In the standard stacking procedure, the first-level regressors are fit to the same training set that is used prepare the inputs for the second-level regressor, which may lead to overfitting. The StackingCVRegressor, however, uses the concept of out-of-fold predictions: the dataset is split into k folds, and in k successive rounds, k-1 folds are used to fit the first level regressor. In each round, the first-level regressors are then applied to the remaining 1 subset that was not used for model fitting in each iteration. The resulting predictions are then stacked and provided -- as input data -- to the second-level regressor. After the training of the StackingCVRegressor, the first-level regressors are fit to the entire dataset for optimal predicitons.
References
- Breiman, Leo. "Stacked regressions." Machine learning 24.1 (1996): 49-64.
- Analogous implementation:
StackingCVClassifier
Example 1: Boston Housing Data Predictions
In this example we evaluate some basic prediction models on the boston housing dataset and see how the and MSE scores are affected by combining the models with StackingCVRegressor. The code output below demonstrates that the stacked model performs the best on this dataset -- slightly better than the best single regression model.
from mlxtend.regressor import StackingCVRegressor
from sklearn.datasets import load_boston
from sklearn.svm import SVR
from sklearn.linear_model import Lasso
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score
import numpy as np
RANDOM_SEED = 42
X, y = load_boston(return_X_y=True)
svr = SVR(kernel='linear')
lasso = Lasso()
rf = RandomForestRegressor(n_estimators=5,
random_state=RANDOM_SEED)
# Starting from v0.16.0, StackingCVRegressor supports
# `random_state` to get deterministic result.
stack = StackingCVRegressor(regressors=(svr, lasso, rf),
meta_regressor=lasso,
random_state=RANDOM_SEED)
print('5-fold cross validation scores:\n')
for clf, label in zip([svr, lasso, rf, stack], ['SVM', 'Lasso',
'Random Forest',
'StackingCVRegressor']):
scores = cross_val_score(clf, X, y, cv=5)
print("R^2 Score: %0.2f (+/- %0.2f) [%s]" % (
scores.mean(), scores.std(), label))
5-fold cross validation scores:
R^2 Score: 0.46 (+/- 0.29) [SVM]
R^2 Score: 0.43 (+/- 0.14) [Lasso]
R^2 Score: 0.53 (+/- 0.28) [Random Forest]
R^2 Score: 0.57 (+/- 0.24) [StackingCVRegressor]
stack = StackingCVRegressor(regressors=(svr, lasso, rf),
meta_regressor=lasso)
print('5-fold cross validation scores:\n')
for clf, label in zip([svr, lasso, rf, stack], ['SVM', 'Lasso',
'Random Forest',
'StackingCVRegressor']):
scores = cross_val_score(clf, X, y, cv=5, scoring='neg_mean_squared_error')
print("Neg. MSE Score: %0.2f (+/- %0.2f) [%s]" % (
scores.mean(), scores.std(), label))
5-fold cross validation scores:
Neg. MSE Score: -33.33 (+/- 22.36) [SVM]
Neg. MSE Score: -35.53 (+/- 16.99) [Lasso]
Neg. MSE Score: -27.08 (+/- 15.67) [Random Forest]
Neg. MSE Score: -25.85 (+/- 17.22) [StackingCVRegressor]
Example 2: GridSearchCV with Stacking
In this second example we demonstrate how StackingCVRegressor works in combination with GridSearchCV. The stack still allows tuning hyper parameters of the base and meta models!
For instance, we can use estimator.get_params().keys() to get a full list of tunable parameters.
from mlxtend.regressor import StackingCVRegressor
from sklearn.datasets import load_boston
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import GridSearchCV
X, y = load_boston(return_X_y=True)
ridge = Ridge(random_state=RANDOM_SEED)
lasso = Lasso(random_state=RANDOM_SEED)
rf = RandomForestRegressor(random_state=RANDOM_SEED)
stack = StackingCVRegressor(regressors=(lasso, ridge),
meta_regressor=rf,
random_state=RANDOM_SEED,
use_features_in_secondary=True)
params = {'lasso__alpha': [0.1, 1.0, 10.0],
'ridge__alpha': [0.1, 1.0, 10.0]}
grid = GridSearchCV(
estimator=stack,
param_grid={
'lasso__alpha': [x/5.0 for x in range(1, 10)],
'ridge__alpha': [x/20.0 for x in range(1, 10)],
'meta_regressor__n_estimators': [10, 100]
},
cv=5,
refit=True
)
grid.fit(X, y)
print("Best: %f using %s" % (grid.best_score_, grid.best_params_))
Best: 0.679151 using {'lasso__alpha': 1.6, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.4}
cv_keys = ('mean_test_score', 'std_test_score', 'params')
for r, _ in enumerate(grid.cv_results_['mean_test_score']):
print("%0.3f +/- %0.2f %r"
% (grid.cv_results_[cv_keys[0]][r],
grid.cv_results_[cv_keys[1]][r] / 2.0,
grid.cv_results_[cv_keys[2]][r]))
if r > 10:
break
print('...')
print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)
0.632 +/- 0.09 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.05}
0.645 +/- 0.08 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.1}
0.641 +/- 0.08 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.15}
0.653 +/- 0.08 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.2}
0.622 +/- 0.10 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.25}
0.630 +/- 0.09 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.3}
0.630 +/- 0.09 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.35}
0.642 +/- 0.09 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.4}
0.654 +/- 0.08 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.45}
0.642 +/- 0.09 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 100, 'ridge__alpha': 0.05}
0.645 +/- 0.09 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 100, 'ridge__alpha': 0.1}
0.648 +/- 0.09 {'lasso__alpha': 0.2, 'meta_regressor__n_estimators': 100, 'ridge__alpha': 0.15}
...
Best parameters: {'lasso__alpha': 1.6, 'meta_regressor__n_estimators': 10, 'ridge__alpha': 0.4}
Accuracy: 0.68
Note
The StackingCVRegressor also enables grid search over the regressors and even a single base regressor. When there are level-mixed hyperparameters, GridSearchCV will try to replace hyperparameters in a top-down order, i.e., regressors -> single base regressor -> regressor hyperparameter. For instance, given a hyperparameter grid such as
params = {'randomforestregressor__n_estimators': [1, 100],
'regressors': [(regr1, regr1, regr1), (regr2, regr3)]}
it will first use the instance settings of either (regr1, regr2, regr3) or (regr2, regr3) . Then it will replace the 'n_estimators' settings for a matching regressor based on 'randomforestregressor__n_estimators': [1, 100].
API
StackingCVRegressor(regressors, meta_regressor, cv=5, shuffle=True, random_state=None, verbose=0, refit=True, use_features_in_secondary=False, store_train_meta_features=False, n_jobs=None, pre_dispatch='2n_jobs', multi_output=False)*
A 'Stacking Cross-Validation' regressor for scikit-learn estimators.
Parameters
-
regressors: array-like, shape = [n_regressors]A list of regressors. Invoking the
fitmethod on theStackingCVRegressorwill fit clones of these original regressors that will be stored in the class attributeself.regr_. -
meta_regressor: objectThe meta-regressor to be fitted on the ensemble of regressor
-
cv: int, cross-validation generator or iterable, optional (default: 5)Determines the cross-validation splitting strategy. Possible inputs for cv are: - None, to use the default 5-fold cross validation, - integer, to specify the number of folds in a
KFold, - An object to be used as a cross-validation generator. - An iterable yielding train, test splits. For integer/None inputs, it will useKFoldcross-validation -
shuffle: bool (default: True)If True, and the
cvargument is integer, the training data will be shuffled at fitting stage prior to cross-validation. If thecvargument is a specific cross validation technique, this argument is omitted. -
random_state: int, RandomState instance or None, optional (default: None)Constrols the randomness of the cv splitter. Used when
cvis integer andshuffle=True. New in v0.16.0. -
verbose: int, optional (default=0)Controls the verbosity of the building process. New in v0.16.0
-
refit: bool (default: True)Clones the regressors for stacking regression if True (default) or else uses the original ones, which will be refitted on the dataset upon calling the
fitmethod. Setting refit=False is recommended if you are working with estimators that are supporting the scikit-learn fit/predict API interface but are not compatible to scikit-learn'sclonefunction. -
use_features_in_secondary: bool (default: False)If True, the meta-regressor will be trained both on the predictions of the original regressors and the original dataset. If False, the meta-regressor will be trained only on the predictions of the original regressors.
-
store_train_meta_features: bool (default: False)If True, the meta-features computed from the training data used for fitting the meta-regressor stored in the
self.train_meta_features_array, which can be accessed after callingfit. -
n_jobs: int or None, optional (default=None)The number of CPUs to use to do the computation.
Nonemeans 1 unless in a :obj:joblib.parallel_backendcontext.-1means using all processors. See :term:Glossary <n_jobs>for more details. New in v0.16.0. -
pre_dispatch: int, or string, optionalControls the number of jobs that get dispatched during parallel execution. Reducing this number can be useful to avoid an explosion of memory consumption when more jobs get dispatched than CPUs can process. This parameter can be: - None, in which case all the jobs are immediately created and spawned. Use this for lightweight and fast-running jobs, to avoid delays due to on-demand spawning of the jobs - An int, giving the exact number of total jobs that are spawned - A string, giving an expression as a function of n_jobs, as in '2*n_jobs'
-
multi_output: bool (default: False)If True, allow multi-output targets, but forbid nan or inf values. If False,
ywill be checked to be a vector. (New in v0.19.0.)
Attributes
-
train_meta_features: numpy array, shape = [n_samples, n_regressors]meta-features for training data, where n_samples is the number of samples in training data and len(self.regressors) is the number of regressors.
Examples
For usage examples, please see https://rasbt.github.io/mlxtend/user_guide/regressor/StackingCVRegressor/
Methods
fit(X, y, groups=None, sample_weight=None)
Fit ensemble regressors and the meta-regressor.
Parameters
-
X: numpy array, shape = [n_samples, n_features]Training vectors, where n_samples is the number of samples and n_features is the number of features.
-
y: numpy array, shape = [n_samples] or [n_samples, n_targets]Target values. Multiple targets are supported only if self.multi_output is True.
-
groups: numpy array/None, shape = [n_samples]The group that each sample belongs to. This is used by specific folding strategies such as GroupKFold()
-
sample_weight: array-like, shape = [n_samples], optionalSample weights passed as sample_weights to each regressor in the regressors list as well as the meta_regressor. Raises error if some regressor does not support sample_weight in the fit() method.
Returns
self: object
fit_transform(X, y=None, fit_params)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params`
and returns a transformed version of `X`.
Parameters
-
X: array-like of shape (n_samples, n_features)Input samples.
-
y: array-like of shape (n_samples,) or (n_samples, n_outputs), default=NoneTarget values (None for unsupervised transformations).
-
**fit_params: dictAdditional fit parameters.
Returns
-
X_new: ndarray array of shape (n_samples, n_features_new)Transformed array.
get_params(deep=True)
Get parameters for this estimator.
Parameters
-
deep: bool, default=TrueIf True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns
-
params: dictParameter names mapped to their values.
predict(X)
Predict target values for X.
Parameters
-
X: {array-like, sparse matrix}, shape = [n_samples, n_features]Training vectors, where n_samples is the number of samples and n_features is the number of features.
Returns
-
y_target: array-like, shape = [n_samples] or [n_samples, n_targets]Predicted target values.
predict_meta_features(X)
Get meta-features of test-data.
Parameters
-
X: numpy array, shape = [n_samples, n_features]Test vectors, where n_samples is the number of samples and n_features is the number of features.
Returns
-
meta-features: numpy array, shape = [n_samples, len(self.regressors)]meta-features for test data, where n_samples is the number of samples in test data and len(self.regressors) is the number of regressors. If self.multi_output is True, then the number of columns is len(self.regressors) * n_targets.
score(X, y, sample_weight=None)
Return the coefficient of determination :math:R^2 of the
prediction.
The coefficient :math:`R^2` is defined as :math:`(1 - \frac{u}{v})`,
where :math:`u` is the residual sum of squares ``((y_true - y_pred)
** 2).sum()and :math:`v` is the total sum of squares((y_true -
y_true.mean()) ** 2).sum()``. The best possible score is 1.0 and it
can be negative (because the model can be arbitrarily worse). A
constant model that always predicts the expected value of y,
disregarding the input features, would get a :math:R^2 score of
0.0.
Parameters
-
X: array-like of shape (n_samples, n_features)Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape
(n_samples, n_samples_fitted), wheren_samples_fittedis the number of samples used in the fitting for the estimator. -
y: array-like of shape (n_samples,) or (n_samples, n_outputs)True values for
X. -
sample_weight: array-like of shape (n_samples,), default=NoneSample weights.
Returns
-
score: float:math:
R^2ofself.predict(X)wrt.y.
Notes
The :math:R^2 score used when calling score on a regressor uses
multioutput='uniform_average' from version 0.23 to keep consistent
with default value of :func:~sklearn.metrics.r2_score.
This influences the score method of all the multioutput
regressors (except for
:class:~sklearn.multioutput.MultiOutputRegressor).
set_params(params)
Set the parameters of this estimator.
Valid parameter keys can be listed with ``get_params()``.
Returns
self
Properties
named_regressors
Returns
List of named estimator tuples, like [('svc', SVC(...))]