BootstrapOutOfBag: A scikit-learn compatible version of the out-of-bag bootstrap

An implementation of the out-of-bag bootstrap to evaluate supervised learning algorithms.

from mlxtend.evaluate import BootstrapOutOfBag

Overview

Originally, the bootstrap method aims to determine the statistical properties of an estimator when the underlying distribution was unknown and additional samples are not available. Now, in order to exploit this method for the evaluation of predictive models, such as hypotheses for classification and regression, we may prefer a slightly different approach to bootstrapping using the so-called Out-Of-Bag (OOB) or Leave-One-Out Bootstrap (LOOB) technique. Here, we use out-of-bag samples as test sets for evaluation instead of evaluating the model on the training data. Out-of-bag samples are the unique sets of instances that are not used for model fitting as shown in the figure below [1].

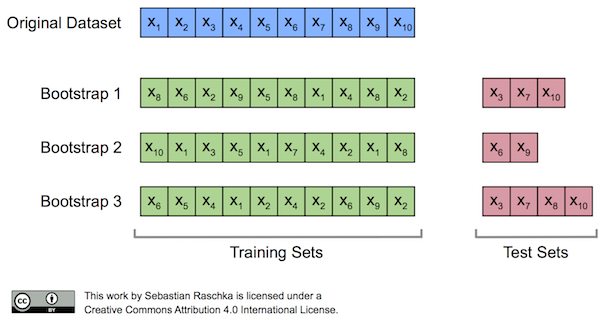
The figure above illustrates how three random bootstrap samples drawn from an exemplary ten-sample dataset ($X_1,X_2, ..., X_{10}$) and their out-of-bag sample for testing may look like. In practice, Bradley Efron and Robert Tibshirani recommend drawing 50 to 200 bootstrap samples as being sufficient for reliable estimates [2].

References

• [1] https://sebastianraschka.com/blog/2016/model-evaluation-selection-part2.html
• [2] Efron, Bradley, and Robert J. Tibshirani. An introduction to the bootstrap. CRC press, 1994. Management of Data (ACM SIGMOD '97), pages 265-276, 1997.

Example 1 -- Evaluating the predictive performance of a model

The BootstrapOutOfBag class mimics the behavior of scikit-learn's cross-validation classes, e.g., KFold:

from mlxtend.evaluate import BootstrapOutOfBag
import numpy as np


oob = BootstrapOutOfBag(n_splits=3)
for train, test in oob.split(np.array([1, 2, 3, 4, 5])):
    print(train, test)

[4 2 1 3 3] [0]
[2 4 1 2 1] [0 3]
[4 3 3 4 1] [0 2]

Consequently, we can use BootstrapOutOfBag objects via the cross_val_score method:

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score

iris = load_iris()
X = iris.data
y = iris.target
lr = LogisticRegression()

print(cross_val_score(lr, X, y))

[ 0.96078431  0.92156863  0.95833333]

print(cross_val_score(lr, X, y, cv=BootstrapOutOfBag(n_splits=3, random_seed=456)))

[ 0.92727273  0.96226415  0.94444444]

In practice, it is recommended to run at least 200 iterations, though:

print('Mean accuracy: %.1f%%' % np.mean(100*cross_val_score(
    lr, X, y, cv=BootstrapOutOfBag(n_splits=200, random_seed=456))))

Mean accuracy: 94.8%

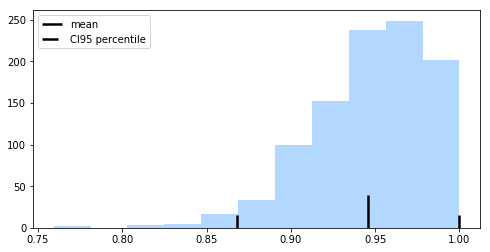
Using the bootstrap, we can use the percentile method to compute the confidence bounds of the performance estimate. We pick our lower and upper confidence bounds as follows:

• $ACC_{lower}$ = $\alpha_1th$ percentile of the $ACC_{boot}$ distribution
• $ACC_{lower}$ = $\alpha_2th$ percentile of the $ACC_{boot}$ distribution

where $\alpha_1 = \alpha$ and $\alpha_2 = 1-\alpha$, and the degree of confidence to compute the $100 \times (1-2 \times \alpha)$ confidence interval. For instance, to compute a 95% confidence interval, we pick $\alpha=0.025$ to obtain the 2.5th and 97.5th percentiles of the b bootstrap samples distribution as the upper and lower confidence bounds.

import matplotlib.pyplot as plt
%matplotlib inline

accuracies = cross_val_score(lr, X, y, cv=BootstrapOutOfBag(n_splits=1000, random_seed=456))
mean = np.mean(accuracies)

lower = np.percentile(accuracies, 2.5)
upper = np.percentile(accuracies, 97.5)

fig, ax = plt.subplots(figsize=(8, 4))
ax.vlines(mean, [0], 40, lw=2.5, linestyle='-', label='mean')
ax.vlines(lower, [0], 15, lw=2.5, linestyle='-.', label='CI95 percentile')
ax.vlines(upper, [0], 15, lw=2.5, linestyle='-.')

ax.hist(accuracies, bins=11,
        color='#0080ff', edgecolor="none", 
        alpha=0.3)
plt.legend(loc='upper left')



plt.show()

API

BootstrapOutOfBag(n_splits=200, random_seed=None)

Parameters

• n_splits : int (default=200)

  Number of bootstrap iterations. Must be larger than 1.

• random_seed : int (default=None)

  If int, random_seed is the seed used by the random number generator.

Returns

• train_idx : ndarray

  The training set indices for that split.

• test_idx : ndarray

  The testing set indices for that split.

Examples

For usage examples, please see https://rasbt.github.io/mlxtend/user_guide/evaluate/BootstrapOutOfBag/

Methods

---

get_n_splits(X=None, y=None, groups=None)

Returns the number of splitting iterations in the cross-validator

Parameters

• X : object

  Always ignored, exists for compatibility with scikit-learn.

• y : object

  Always ignored, exists for compatibility with scikit-learn.

• groups : object

  Always ignored, exists for compatibility with scikit-learn.

Returns

• n_splits : int

  Returns the number of splitting iterations in the cross-validator.

---

split(X, y=None, groups=None)

y : array-like or None (default: None) Argument is not used and only included as parameter for compatibility, similar to KFold in scikit-learn.

• groups : array-like or None (default: None)

  Argument is not used and only included as parameter for compatibility, similar to KFold in scikit-learn.