mcnemar_table: Contingency table for McNemar's test

Function to compute a 2x2 contingency table for McNemar's Test

from mlxtend.evaluate import mcnemar_table

Overview

contingency Table for McNemar's Test

A 2x2 contingency table as being used in a McNemar's Test (mlxtend.evaluate.mcnemar) is a useful aid for comparing two different models. In contrast to a typical confusion matrix, this table compares two models to each other rather than showing the false positives, true positives, false negatives, and true negatives of a single model's predictions:

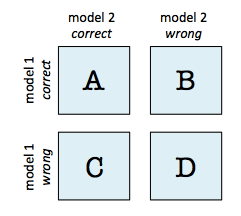
For instance, given that 2 models have a accuracy of with a 99.7% and 99.6% a 2x2 contingency table can provide further insights for model selection.

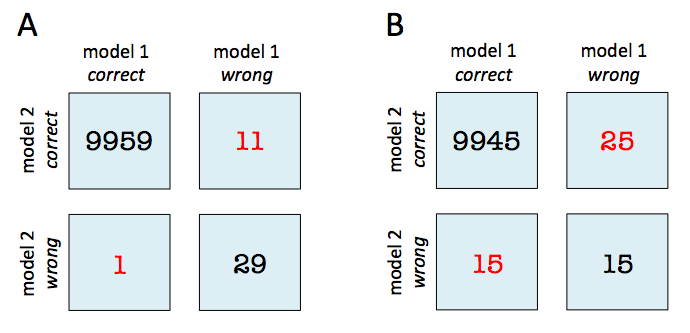
In both subfigure A and B, the predictive accuracies of the two models are as follows:

• model 1 accuracy: 9,960 / 10,000 = 99.6%
• model 2 accuracy: 9,970 / 10,000 = 99.7%

Now, in subfigure A, we can see that model 2 got 11 predictions right that model 1 got wrong. Vice versa, model 2 got 1 prediction right that model 2 got wrong. Thus, based on this 11:1 ratio, we may conclude that model 2 performs substantially better than model 1. However, in subfigure B, the ratio is 25:15, which is less conclusive about which model is the better one to choose.

References

• McNemar, Quinn, 1947. "Note on the sampling error of the difference between correlated proportions or percentages". Psychometrika. 12 (2): 153–157.
• Edwards AL: Note on the “correction for continuity” in testing the significance of the difference between correlated proportions. Psychometrika. 1948, 13 (3): 185-187. 10.1007/BF02289261.
• https://en.wikipedia.org/wiki/McNemar%27s_test

Example 2 - 2x2 contingency Table

import numpy as np
from mlxtend.evaluate import mcnemar_table

y_true = np.array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])

y_mod1 = np.array([0, 1, 0, 0, 0, 1, 1, 0, 0, 0])
y_mod2 = np.array([0, 0, 1, 1, 0, 1, 1, 0, 0, 0])

tb = mcnemar_table(y_target=y_true, 
                   y_model1=y_mod1, 
                   y_model2=y_mod2)

tb

array([[4, 1],
       [2, 3]])

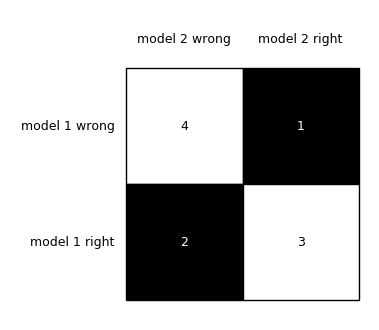
To visualize (and better interpret) the contingency table via matplotlib, we can use the checkerboard_plot function:

from mlxtend.plotting import checkerboard_plot
import matplotlib.pyplot as plt

brd = checkerboard_plot(tb,
                        figsize=(3, 3),
                        fmt='%d',
                        col_labels=['model 2 wrong', 'model 2 right'],
                        row_labels=['model 1 wrong', 'model 1 right'])
plt.show()

API

mcnemar_table(y_target, y_model1, y_model2)

Compute a 2x2 contingency table for McNemar's test.

Parameters

• y_target : array-like, shape=[n_samples]

  True class labels as 1D NumPy array.

• y_model1 : array-like, shape=[n_samples]

  Predicted class labels from model as 1D NumPy array.

• y_model2 : array-like, shape=[n_samples]

  Predicted class labels from model 2 as 1D NumPy array.

Returns

• tb : array-like, shape=[2, 2]

  2x2 contingency table with the following contents: a: tb[0, 0]: # of samples that both models predicted correctly b: tb[0, 1]: # of samples that model 1 got right and model 2 got wrong c: tb[1, 0]: # of samples that model 2 got right and model 1 got wrong d: tb[1, 1]: # of samples that both models predicted incorrectly

Examples

For usage examples, please see https://rasbt.github.io/mlxtend/user_guide/evaluate/mcnemar_table/