bootstrap_point632_score: The .632 and .632+ boostrap for classifier evaluation

An implementation of the .632 bootstrap to evaluate supervised learning algorithms.

from mlxtend.evaluate import bootstrap_point632_score

Overview

Originally, the bootstrap method aims to determine the statistical properties of an estimator when the underlying distribution was unknown and additional samples are not available. Now, in order to exploit this method for the evaluation of predictive models, such as hypotheses for classification and regression, we may prefer a slightly different approach to bootstrapping using the so-called Out-Of-Bag (OOB) or Leave-One-Out Bootstrap (LOOB) technique. Here, we use out-of-bag samples as test sets for evaluation instead of evaluating the model on the training data. Out-of-bag samples are the unique sets of instances that are not used for model fitting as shown in the figure below [1].

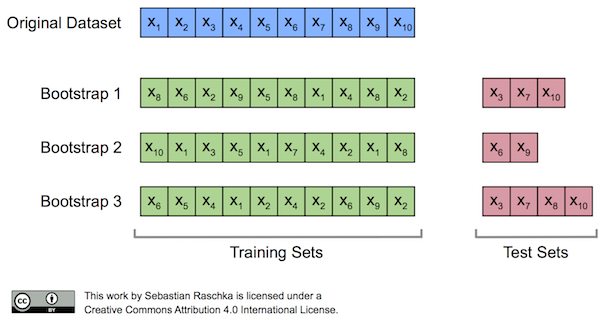
The figure above illustrates how three random bootstrap samples drawn from an exemplary ten-sample dataset ( $X_1,X_2, ..., X_{10}$ ) and their out-of-bag sample for testing may look like. In practice, Bradley Efron and Robert Tibshirani recommend drawing 50 to 200 bootstrap samples as being sufficient for reliable estimates [2].

.632 Bootstrap

In 1983, Bradley Efron described the .632 Estimate, a further improvement to address the pessimistic bias of the bootstrap cross-validation approach described above [3]. The pessimistic bias in the "classic" bootstrap method can be attributed to the fact that the bootstrap samples only contain approximately 63.2% of the unique samples from the original dataset. For instance, we can compute the probability that a given sample from a dataset of size n is not drawn as a bootstrap sample as

$P (\text{not chosen}) = \bigg(1 - \frac{1}{n}\bigg)^n,$

which is asymptotically equivalent to $\frac{1}{e} \approx 0.368$ as $n \rightarrow \infty.$

Vice versa, we can then compute the probability that a sample is chosen as $P (\text{chosen}) = 1 - \bigg(1 - \frac{1}{n}\bigg)^n \approx 0.632$ for reasonably large datasets, so that we'd select approximately $0.632 \times n$ uniques samples as bootstrap training sets and reserve $0.368 \times n$ out-of-bag samples for testing in each iteration.

Now, to address the bias that is due to this the sampling with replacement, Bradley Efron proposed the .632 Estimate that we mentioned earlier, which is computed via the following equation:

$\text{ACC}_{boot} = \frac{1}{b} \sum_{i=1}^b \big(0.632 \cdot \text{ACC}_{h, i} + 0.368 \cdot \text{ACC}_{train}\big),$

where $\text{ACC}_{train}$ is the accuracy computed on the whole training set, and $\text{ACC}_{h, i}$ is the accuracy on the out-of-bag sample.

.632+ Bootstrap

Now, while the .632 Boostrap attempts to address the pessimistic bias of the estimate, an optimistic bias may occur with models that tend to overfit so that Bradley Efron and Robert Tibshirani proposed the The .632+ Bootstrap Method (Efron and Tibshirani, 1997). Instead of using a fixed "weight" $\omega = 0.632$ in

$ACC_{\text{boot}} = \frac{1}{b} \sum_{i=1}^b \big(\omega \cdot \text{ACC}_{h, i} + (1-\omega) \cdot \text{ACC}_{train} \big),$

we compute the weight $\gamma$ as

$\omega = \frac{0.632}{1 - 0.368 \times R},$

where R is the relative overfitting rate

$R = \frac{(-1) \times (\text{ACC}_{h, i} - \text{ACC}_{train})}{\gamma - (1 -\text{ACC}_{h, i})}.$

(Since we are plugging $\omega$ into the equation for computing $ACC_{boot}$ that we defined above, $\text{ACC}_{h, i}$ and $\text{ACC}_{train}$ still refer to the out-of-bag accuracy in the ith bootstrap round and the whole training set accuracy, respectively.)

Further, we need to determine the no-information rate $\gamma$ in order to compute R. For instance, we can compute $\gamma$ by fitting a model to a dataset that contains all possible combinations between samples $x_{i'}$ and target class labels $y_{i}$ — we pretend that the observations and class labels are independent:

$\gamma = \frac{1}{n^2} \sum_{i=1}^{n} \sum_{i '=1}^{n} L(y_{i}, f(x_{i '})).$

Alternatively, we can estimate the no-information rate $\gamma$ as follows:

$\gamma = \sum_{k=1}^K p_k (1 - q_k),$

where $p_k$ is the proportion of class $k$ samples observed in the dataset, and $q_k$ is the proportion of class $k$ samples that the classifier predicts in the dataset.

References

[1] https://sebastianraschka.com/blog/2016/model-evaluation-selection-part2.html
[2] Efron, Bradley, and Robert J. Tibshirani. An introduction to the bootstrap. CRC press, 1994. Management of Data (ACM SIGMOD '97), pages 265-276, 1997. [3] Efron, Bradley. 1983. “Estimating the Error Rate of a Prediction Rule: Improvement on Cross-Validation.” Journal of the American Statistical Association 78 (382): 316. doi:10.2307/2288636.
[4] Efron, Bradley, and Robert Tibshirani. 1997. “Improvements on Cross-Validation: The .632+ Bootstrap Method.” Journal of the American Statistical Association 92 (438): 548. doi:10.2307/2965703.

Example 1 -- Evaluating the predictive performance of a model via the classic out-of-bag Bootstrap

The bootstrap_point632_score function mimics the behavior of scikit-learn's `cross_val_score, and a typically usage example is shown below:

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from mlxtend.evaluate import bootstrap_point632_score
import numpy as np

iris = datasets.load_iris()
X = iris.data
y = iris.target
tree = DecisionTreeClassifier(random_state=123)

# Model accuracy
scores = bootstrap_point632_score(tree, X, y, method='oob')
acc = np.mean(scores)
print('Accuracy: %.2f%%' % (100*acc))


# Confidence interval
lower = np.percentile(scores, 2.5)
upper = np.percentile(scores, 97.5)
print('95%% Confidence interval: [%.2f, %.2f]' % (100*lower, 100*upper))

Accuracy: 94.45%
95% Confidence interval: [87.71, 100.00]

Example 2 -- Evaluating the predictive performance of a model via the .632 Bootstrap

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from mlxtend.evaluate import bootstrap_point632_score
import numpy as np

iris = datasets.load_iris()
X = iris.data
y = iris.target
tree = DecisionTreeClassifier(random_state=123)

# Model accuracy
scores = bootstrap_point632_score(tree, X, y)
acc = np.mean(scores)
print('Accuracy: %.2f%%' % (100*acc))


# Confidence interval
lower = np.percentile(scores, 2.5)
upper = np.percentile(scores, 97.5)
print('95%% Confidence interval: [%.2f, %.2f]' % (100*lower, 100*upper))

Accuracy: 96.42%
95% Confidence interval: [92.41, 100.00]

Example 3 -- Evaluating the predictive performance of a model via the .632+ Bootstrap

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from mlxtend.evaluate import bootstrap_point632_score
import numpy as np

iris = datasets.load_iris()
X = iris.data
y = iris.target
tree = DecisionTreeClassifier(random_state=123)

# Model accuracy
scores = bootstrap_point632_score(tree, X, y, method='.632+')
acc = np.mean(scores)
print('Accuracy: %.2f%%' % (100*acc))


# Confidence interval
lower = np.percentile(scores, 2.5)
upper = np.percentile(scores, 97.5)
print('95%% Confidence interval: [%.2f, %.2f]' % (100*lower, 100*upper))

Accuracy: 96.29%
95% Confidence interval: [91.86, 98.92]

API

bootstrap_point632_score(estimator, X, y, n_splits=200, method='.632', scoring_func=None, predict_proba=False, random_seed=None, clone_estimator=True)

Implementation of the .632 [1] and .632+ [2] bootstrap for supervised learning

References:

- [1] Efron, Bradley. 1983. "Estimating the Error Rate
of a Prediction Rule: Improvement on Cross-Validation."
Journal of the American Statistical Association
78 (382): 316. doi:10.2307/2288636.
- [2] Efron, Bradley, and Robert Tibshirani. 1997.
"Improvements on Cross-Validation: The .632+ Bootstrap Method."
Journal of the American Statistical Association
92 (438): 548. doi:10.2307/2965703.

Parameters

estimator : object

An estimator for classification or regression that follows the scikit-learn API and implements "fit" and "predict" methods.
X : array-like

The data to fit. Can be, for example a list, or an array at least 2d.
y : array-like, optional, default: None

The target variable to try to predict in the case of supervised learning.
n_splits : int (default=200)

Number of bootstrap iterations. Must be larger than 1.
method : str (default='.632')

The bootstrap method, which can be either - 1) '.632' bootstrap (default) - 2) '.632+' bootstrap - 3) 'oob' (regular out-of-bag, no weighting) for comparison studies.
scoring_func : callable,

Score function (or loss function) with signature scoring_func(y, y_pred, **kwargs). If none, uses classification accuracy if the

estimator is a classifier and mean squared error if the estimator is a regressor.

predict_proba : bool

Whether to use the predict_proba function for the estimator argument. This is to be used in conjunction with scoring_func which takes in probability values instead of actual predictions. For example, if the scoring_func is :meth:sklearn.metrics.roc_auc_score, then use predict_proba=True. Note that this requires estimator to have predict_proba method implemented.
random_seed : int (default=None)

If int, random_seed is the seed used by the random number generator.
clone_estimator : bool (default=True)

Clones the estimator if true, otherwise fits the original.

Returns

scores : array of float, shape=(len(list(n_splits)),)

Array of scores of the estimator for each bootstrap replicate.

Examples

    >>> from sklearn import datasets, linear_model
    >>> from mlxtend.evaluate import bootstrap_point632_score
    >>> iris = datasets.load_iris()
    >>> X = iris.data
    >>> y = iris.target
    >>> lr = linear_model.LogisticRegression()
    >>> scores = bootstrap_point632_score(lr, X, y)
    >>> acc = np.mean(scores)
    >>> print('Accuracy:', acc)
    0.953023146884
    >>> lower = np.percentile(scores, 2.5)
    >>> upper = np.percentile(scores, 97.5)
    >>> print('95%% Confidence interval: [%.2f, %.2f]' % (lower, upper))
    95% Confidence interval: [0.90, 0.98]

    For more usage examples, please see
    https://rasbt.github.io/mlxtend/user_guide/evaluate/bootstrap_point632_score/

Keys	Action
`?`	Open this help
`n`	Next page
`p`	Previous page
`s`	Search